2/10に、広尾学園小石川の入試結果が公開されました。
https://hiroo-koishikawa.ed.jp/hk/wp-content/uploads/2022/02/46b7fed9707bf38cac2b130b43ab672f.pdf
https://hiroo-koishikawa.ed.jp/hk/wp-content/uploads/2022/03/37f9cde4787cd49194f4c893cad13442.pdf
↑上記pdfは削除されたようです。
2月入試の応募者数・受験者数はともに昨年を上回っていますが、合格者数は昨年の341名から205名に大幅に減りました(4割減)。
特に2/1の午前・午後の合格者数が昨年の半分程度になりました。
以下、入試結果について、昨年と今年の比較を当方の勝手な考察を含めて書いていきます。
昨年と今年の比較⓵合格者数、実質倍率
昨年と今年(2/10時点)の合格者数は以下です。(単位:人。SG・本科合計)
| 2/1 AM | 2/1 PM | 2/2 | 2/3 | 2/4 一般 | 2/4 AG | 合計 | |
| 定員 | 30 | 20 | 10 | 10 | 10 | 10 | 90 |
| 2021年 | 84 | 128 | 39 | 45 | 39 | 6 | 341 |
| 2022年 | 41 | 63 | 35 | 33 | 31 | 2 | 205 |
| 増減 | ▲43 | ▲65 | ▲4 | ▲12 | ▲8 | ▲4 | ▲136 |
2021年と比較して、2/2あたりは合格者数は微減程度ですが、2/1は午前・午後ともに合格者数が昨年のほぼ半分に抑えられています。
もちろん実質倍率も昨年の2/1午前2.3倍、2/1午後3.3倍から、それぞれ7.2倍、6.9倍に高騰しています。(単位:倍)
| 2/1 AM | 2/1 PM | 2/2 | 2/3 | 2/4 一般 | 2/4 AG | |
| 2021年 | 2.3 | 3.3 | 7.9 | 8.1 | 10.0 | 5.8 |
| 2022年 | 7.2 | 6.9 | 9.6 | 12.4 | 14.8 | 20.0 |
なお、2021年、2022年ともに募集要項にて合格見込数が記載されていましたが、2021年は合格見込数500名(⇒実績341)、2022年は350名(⇒実績204名)でした。
以下予想でしかないですが、昨年の2/1午前・午後の歩留まり率が予想以上に高かった関係で、今年は学校のキャパシティを考慮して絞ったのでしょうか・・・
ただ、そうすると、募集要項に記載の2月合格見込数350名については、既に2月入試開始前から実際の合格者はこれよりも大幅に減らす想定だったように思われます。
2021年が定員120名に対して198名入学(本科2クラス追加)したため2022年は合格者を絞るのではないかという質問に対し、学校説明会では、2022年にも仮に198名入学したとしても、中庭を潰して校舎を増築するので問題ないような話っぷりでしたが・・・
昨年と今年の比較②平均点
以下、昨年(2021年)と今年(2022年)の本科コースで比較してみます。
(単位:点、小数点以下切り捨て。なお、合格者平均点はSG⇒本科スライド合格者を含む)
○2021年
| 2/1 AM | 2/1 PM | 2/2 | 2/3 | 2/4 一般 | |
| 受験者平均点 | 164 | 114 | 114 | 99 | 107 |
| 合格者平均点 | 190 | 146 | 149 | 136 | 140 |
| 合格最低点 | 164 | 131 | 137 | 131 | 136 |
| 実質倍率 | 2.3 | 3.3 | 7.9 | 8.1 | 10.0 |
○2022年
| 2/1 AM | 2/1 PM | 2/2 | 2/3 | 2/4 一般 | |
| 受験者平均点 | 150 | 113 | 138 | 126 | 108 |
| 合格者平均点 | 192 | 145 | 158 | 160 | 147 |
| 合格最低点 | 179 | 135 | 138 | 131 | 124 |
| 実質倍率 | 7.2 | 6.9 | 9.6 | 12.4 | 14.8 |
2/1AMは受験者平均点は昨年より低下しています(おそらく問題が難化したため)が、合格者数を絞ったため、合格者平均点はほぼ同じ、合格最低点は15点も上昇しているように見えます。
ただ、2/1PMは受験者平均点・合格者平均点・合格最低点いずれも昨年と大差なく、それでいて実質倍率は倍以上になっているように見えますが・・・
よく分からないのが2/2です。
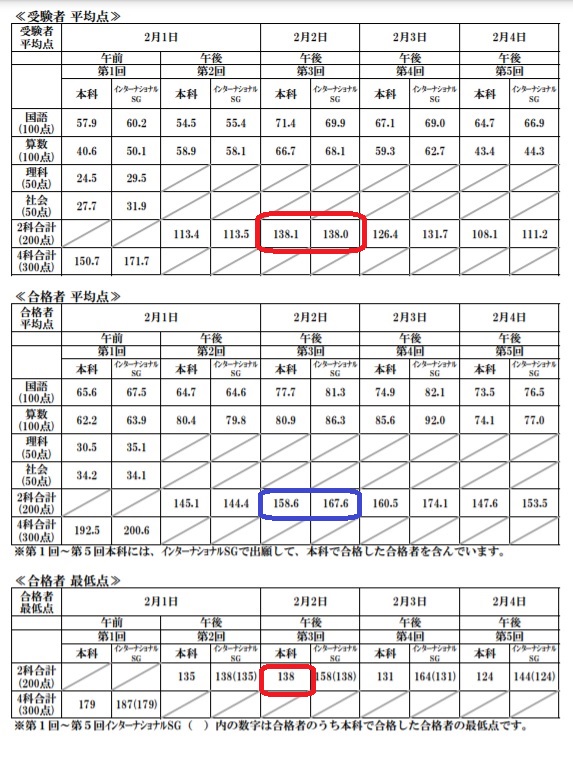
受験者平均点が138点、合格最低点が138点。つまり受験者平均点を取れば合格、ということになるもですが・・・
2021年の2/1AMのように実質倍率が2倍程度なら、これは普通にある話です。
ただ、2022年2/2の場合、実質倍率は9.6倍です。
ここで、単純化して、仮に2/2の実質倍率10倍、受験者数20名、合格者数2名とします(実際には336名受験、35名合格)。
本科の合格者平均は158点なので、仮に138点(合格最低点)と178点の人が合格とします。
このとき、残り18名の(不合格者)平均点は以下になります。
(138(受験者平均点)x20 – ( 138 + 178 )) ÷ 18 =135.8
不合格=全員138点以下であるため、不合格者は(不合格者平均点を押し上げる)136点~138点の人が大半にならないと計算が合いません。
2/3も実質倍率が12.4倍なのに受験者平均点+5点で合格?というのも疑問があります。
3/6追記:やはり間違いだったようです。
修正後は以下。
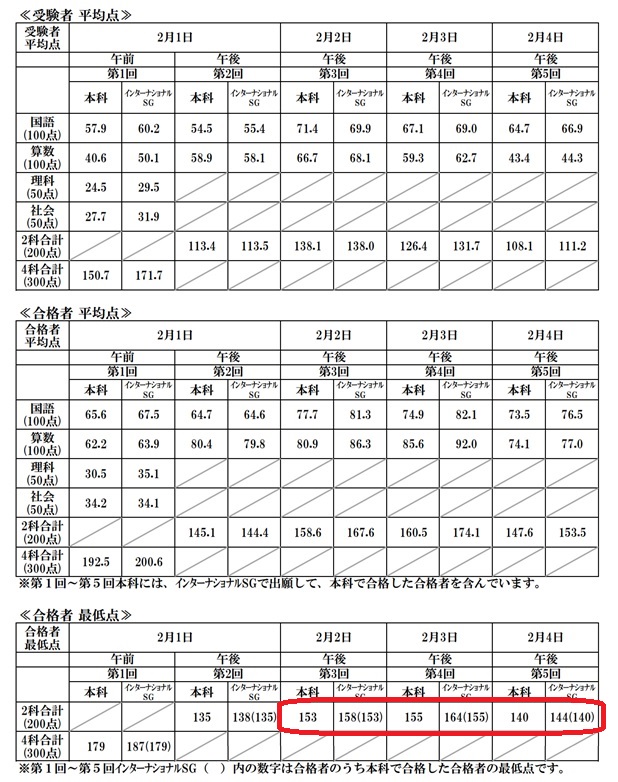
修正箇所:2/2~2/4合格者最低点
- 2/2午後:138⇒153
- 2/3午後:131⇒155
- 2/4午後:124⇒140
・・・昨年も、当初の入試結果では、2/4の合格者平均点は140.1点、合格者最低点は146点という、理屈としてはあり得ない(合格者平均点>合格者最低点になるべき)情報になっていて、翌日か翌々日に訂正されていましたので、今回も間違いかもしれないので、ここまでにします。
つまり、2021年と全く同じ間違いを2022年もやってた、ということです。
詳細は下記記事のとおりです。
昨年と全く同様の間違いで、しかも、昨年は2/8に早々に修正しているのに、今年は2/10公開後、約1ヶ月後の3/5になってやっと修正しているのは全く解せないです。
ところで、2/2および2/3の合格者平均点は160点前後、つまり8割正答となります。
他の日程も含め、算数の受験者平均点・合格者平均点の上昇によるものかと思いますので、以下掘り下げてみます。
昨年と今年の比較③算数の平均点
本題に入る前に、以下、問題です。
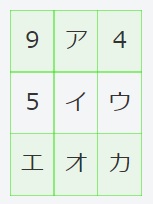
次の9つのマスに異なる整数を入れて縦、横、ななめに並ぶ数の和がすべて等しくなるようにします。ア、イ、ウ、エ、オ、カに入る数をそれぞれ求めなさい。
| 9 | ア | 4 |
| 5 | イ | ウ |
| エ | オ | カ |
保護者の方も、おそらく、魔方陣自体はどこかで見たことがあるとは思いますが、分かりますか?
解説は後回しにするので、とりあえず少し考えてみてください。
さて。
以下、算数についても昨年(2021年)と今年(2022年)の本科コースで比較してみます。
(単位:点、小数点以下切り捨て。なお、合格者平均点はSG⇒本科スライド合格者を含む)
○2021年
| 2/1 AM | 2/1 PM | 2/2 | 2/3 | 2/4 一般 | |
| 受験者平均点 | 46 | 48 | 46 | 42 | 40 |
| 合格者平均点 | 59 | 71 | 71 | 63 | 64 |
| 平均点の差 | 13 | 23 | 25 | 21 | 24 |
○2022年
| 2/1 AM | 2/1 PM | 2/2 | 2/3 | 2/4 一般 | |
| 受験者平均点 | 40 | 58 | 66 | 59 | 43 |
| 合格者平均点 | 62 | 80 | 80 | 85 | 74 |
| 平均点の差 | 22 | 22 | 14 | 26 | 31 |
広尾学園小石川に限らず算数は差がつく教科ではありますが、昨年同様、今年も算数でかなり決まってしまう入試だったように見えます(表は割愛しますが、今年の国語の合格者平均点マイナス受験者平均点はほぼ10点以下でした)。
特に2/1AM以外は、当方は問題は見ていないのですが、合格者平均が8割(2/3は85%、SG合格者平均に至っては92%)ぐらいなので、算数が得意でないと厳しい入試だったはずです。
また、受験者平均点から見ても、おそらく昨年より受験者の持ち偏差値がかなり上昇したと思われます。
さて、2/1AMだけは当方も問題を入手できた(昨年分は四谷大塚過去問データベース、今年分はインターエデュ)ので、比較してみると、今年の方が算数の問題はかなり難しくなった印象です。
よって、2/1AMの算数の受験者平均点が昨年より低下したのは、昨年のようにどこかの大手塾の受験生がR4偏差値だけ見て大挙押し寄せてしまったため、ではないと思います。
なお、問題難化にも関わらず合格者平均点が上昇したのは、合格者数の減少(実質倍率の上昇)のためかと思われます。
ここまで、問題難化というのは、あくまで当方がそう感じただけなのですが、
例えば、大問2の(2)で、これが少し上で記載した問題です。(大問1は計算、大問2は小問集合)
以下、再掲です。
次の9つのマスに異なる整数を入れて縦、横、ななめに並ぶ数の和がすべて等しくなるようにします。ア、イ、ウ、エ、オ、カに入る数をそれぞれ求めなさい。
| 9 | ア | 4 |
| 5 | イ | ウ |
| エ | オ | カ |
魔方陣で、9つのマスに異なる整数を入れるとの記載があって、既に4と5と9が埋まっていることから・・・
「1~9を埋めるのだから、1+2+・・・+9=45、よって1列の和は45÷3=15。だからアは15-9-4=2、エは15-9-4=1。次にイは15-4-1=10?それだと9+イ+カ=19+カ、あれ?15にならない・・・」
結構多くの人がこんな感じで詰まってしまうように思います。
原因は・・・どこにも「1~9を埋める」なんて書いていませんよね。
ちなみに1~9のみを使う魔方陣は、以下のように実在します(なので、上記のように勘違いする)。
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
ここでは詳細は割愛しますが、1~9のみを使う魔方陣は、真ん中が5、あとの数字は上図、もしくは回転・反転したものしかありません。
今回の問題では既に5は真ん中以外で使用しているので、上図のようにはなりません。
では、どう解くかというと・・・
当方が書く以前に、ほぼ同様の問題をすごく分かりやすく解説しているサイトがありましたので、まずはそちらへのリンクをさせていただきます。
以下、今回の問題の場合です。
| 9 | ア | 4 |
| 5 | イ | ウ |
| エ | オ | カ |
(左縦)9+5+エ=(左下がりの斜め)4+イ+エ
ここで、エは共通なので、イ=9+5-4=10 になります。
次に、(*)
(右下がりの斜め)9+10+カ=(右縦)4+ウ+カ
ここで、カは共通なので、ウ=9+10-4=15 になります。
すると、中横=5+10+15=30で、1列の和は30になります。
1列の和が求まれば、残りは簡単に求まるので省略します。
(*)(中横)5+10+ウ=(右縦)4+ウ+カでカ=5+10-4=11、(右下がりの斜め)9+10+11=30、でも求まります。
おそらく、同様の問題を1度でも解いたことがある人はすぐ分かったかと思いますが、35年前ぐらいの中学受験と20年前ぐらいの「算チャレ」(算数にチャレンジ)で時代が止まっていた当方には新鮮な問題だったので、当サイトでは珍しく問題を解説してみました。
かなり話がそれてしまったので、今回はここまでにします。
今回の入試結果は、入学金納入期限(2/9)の後の2/10に公開されており、おそらく入学者数はほぼ固まっているかと思いますので、今年の広尾学園小石川の記事は本記事まで、になるはずです。
次回は、合格者4割減にも関わらず昨年より合格者を増やした、どこかの大手塾の実績R4偏差値がどの程度予想R4偏差値とずれていたか、の確認になります。





コメント